The Forward View of TD ( $\lambda$ )

이 방식은 여러개의 n-step return을 사용 하는 방식이다.

이 여러개의 n-step return 들에게 특이한 가중 평균을 적용한다.

Complex Backup

여러개의 n-step return 을 사용하여 update(?) 하는 것을 Complex Backup 이라고 한다.

간단한 Complex Backup

이해를 돕기 위해 간단한 Complex Backup 을 예를 든다면, 아래 그림과 같다.

책 예제

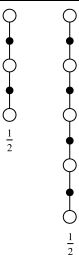
위 예제는 2 개의 n-step return 을 사용했고,

가장 간단한 평균 방법, 즉, n개를 더하여 n으로 나눈방법을 사용했다.

하나의 n-step return 는 TD backup-diagram 으로 표시할 수 있다.

평균의 일반화

그냥 평균은 가중 평균으로 일반화 할 수 있다.

(a+b+c) / 3 = 1/3a + 1/3b + 1/3c

위의 단순 산술 평균은 가중 평균으로 보았을 때 가중치가 1/3 인 것이다.

책의 간단한 Complex Backup 예제는 가중 평균으로 보면, 1/2 이 가중치이다.

TD($\lambda$) 가중 평균 가중치

TD($\lambda$) 가중 평균 가중치는 아래와 같다.

$(1-\lambda) \lambda^ {n-1}$

$0 \le \lambda \le 1$

등비 수열 개념으로도 볼 수 있다.

초항이 $(1-\lambda)$ 이고, 공비가 $\lambda$ 이다.

TD($\lambda$)

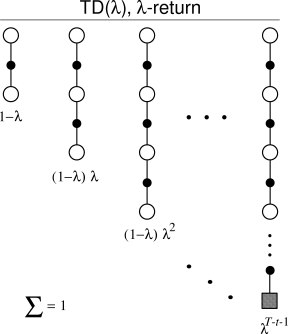
위의 그림은 여러 개의 n-step return 들이 있고,

각각, 가중 평균 가중치가 밑에 나와 있다.

$\lambda$-Return

위의 그림을 식으로 나타내면 다음의 식으로 만들 수 있다.

첫 번째, 무수히 많은 경우

$R_{t}^{\lambda} = (1-\lambda) \sum_{n=1}^{\infty} \lambda ^{n-1} R_{t}^{(n)}$

episod 가 존재할 경우

$R_{t}^{\lambda} = (1-\lambda) \sum_{n=1}^{T-t-1} \lambda ^{n-1} R_{t}^{(n)} + \lambda^{T-t-1}R_{t} \$

뒤에 더해진 것은 MC 의 n-step return 으로 볼 수 있다.

일반화

재미있는 것은 ,

위의 식에서 $\lambda$ 를 1으로 하면,

$(1-\lambda)$ 때문에 맨 뒤에 것 ( MC n-step return ) 만 남고 모두 0 이 된다.

즉 , MC 가 된다.

위의 식에서 $\lambda$ 를 0으로 하면,

첫 번째 것만 남고 모두 0 이 된다.

(수열의 첫 항만 빼고 모두 $\lambda$ , 즉 0 이 곱해진다. )

첫 번째 것은 TD(0) n-step return , 즉 one-step return 이다.

즉 , TD(0) 가 된다.

$\lambda$-Return Alogrithm

update 방식이 아래 식과 같이 될 것 같다.

$\bigtriangleup V_{t}(s_{t}) = \alpha [ R_{t}^{\lambda} -V_{t}(s_{t} )]$

on-line, off-line 모두 사용가능하다고 한다.

이론적 관점

지금까지는 이론적 관점이다.

실제 알고리즘은 위의 말처럼 구현 되어 있지 않는 것 같다.

실제 알고리즘은 다음에 나올 Backward 관점은 즉, Mechanistic 관점으로 볼 수 있다.