Coarse Coding

연속적이고, 2 차원인 상태 집합을 가정하자.

이 경우 상태는 이 차원 벡터로 볼 수 있다.

또한 2차원 공간의 한 점으로 볼 수 있다.

이런 경우 여러 feature 중에 하나는 그림 8.2 에서 처럼 '상태 공간'에서 '원' 과 대응시킬 수 있다. (?).

어떤 상태가 원 안에 있다면, 해당 feature는 1 이고, 이때를 'present' 상태로 볼 수 있다.

반대로 원 안에 없으면, feature 값은 0 이고, 'absent' 라고 하자

이렇게 두 가지 경우만 가능한 feature 를 binary feature 라고 한다.

주어진 어떤 한 상태의 여러 binary feature 들이 'present' 이면, 이 상태는 여러 원 안에 있다는 의미이고, 이는 상태의 위치를 '거칠게' ( coarsely ) 부호화(code) 시켰다.

하나의 상태를 여러 중첩된 feature 들로 표현하는 것을 'coarse coding' 이라고 한다.

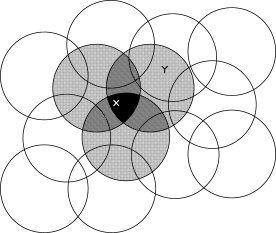figure 8.2 : Coarse Coding

선형 경사 하강 추정 기법을 가정하면, 크기와 원들의 밀도의 영향을 고려해야 한다.(?)

연관된(?) 각 원은 학습으로 영향 받는 parameter ( $$ \vec { \theta } _t 의 요소 ) 들이다.

한 점(상태) X 를 학습시키면, X 를 포함하는 원의 parameter 들 모두가 영향 받는다.

따라서, 식 8.8 에 의해서 기대값(value function) 의 추정은 관련된 원들 위의 모든 점들에 의해서 영향을 받는다.

한 점에 겹쳐진 원들이 많을 수록 그 영향도 커진다.

원의 크기가 작으면, 일반화도 작아진다. 그림 8.3a 참조 (?)

반대로, 원의 크기가 크면, 일반화도 넓은 곳에 미친다. 8.3b 참조

더욱이, 모양도 일반화의 영향을 미친다.

예를 들어 완벽한 원이 아니고, 한 쪽으로 긴 타원 모양이면, 일반화(?)도 비슷하게 영향 받는다. 8.3c

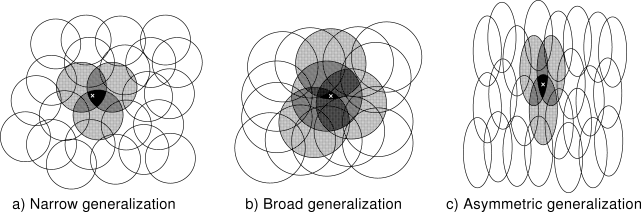그림 8.3

receptive field 이 넓으면, 즉, 원의 넓이가 넓어지면, 일반화되는 영역도 넓어진다.

하지만, 추정의 정확도는, 원으로 구분되는 영역이 세세하지 않으므로 정밀하지 않게 된다.

행복하게도(?) 이것은(?) 그 케이스(?)가 아니다. (?)

한 점에서 다른 점의 초기 일반화는 receptive field 의 크기와 모양으로 제어된다. (?)

하지만, 정밀한 분별(?)은 모든 feature 의 개수로 더욱 제어된다. (?)

...

results matching ""